[리뷰] 수학이 막히면 깨봉 수학
in Review on Review, Book, 분모0, 계산없이, 루트, 왜, 로그, 이미지, 방정식, 수학머리, 원넓이, 직관, 기하학, 함수, 수열, 미분, 경우의수, 평균, 농도

매경주니어북스출판사의"수학이 막히면 깨봉 수학(조봉한 저)"를 읽고 작성한 리뷰입니다.

프레임을 새롭게 바꿔 창의적이고 직관적인 방법으로 수학에 숨은 원리를 깨우치게 해주는 책이다.
깨봉 수학은 이미 유튜브 채널 깨봉수학로 유명하다. 링크를 클릭하여 아무 영상이나 시청해보면 책에 숨겨진 가치를 바로 확인할 수 있다. 그동안 우리가 수학에 몰랐던 원리가 얼마나 많이 담겨있는지 실감할 수 있다.
학교에서는 평가와 변별력을 이유로 학생들에게 성능 좋은 계산기가 되기를 강요했다. 정해진 시간에 빨리 풀 수 있어야 했고, 나아가 계산 기능을 향상 시키기 위해 그 속에 숨겨진 원리는 등한시하고 빠르게 공식을 외워야 원하는 점수를 얻을 수 있었다.
AI에는 경사하강법이라는 개념이 나온다. 이미 다른 분야에서도 최적화 개념으로 활용되어 왔지만 그 근원이 무엇이든 간에 인공지능을 학습시키는 핵심 개념이며 여기에 미분이 활용된다. 미분을 어떻게 활용하느냐에 따라 알파고와 같은 AI를 만들 수 있는데 이런 세상을 바꾸는 원리를 찾아내는 능력이 우리에겐 부족하다.
저자는 우리 교육과정에 포함되지 않은 미국과 같은 기초학문이 튼튼한 나라의 원리 및 역사 그리고 본인 스스로 AI 전문가가 되기 까지 익혀온 인사이트를 접목하여 수학을 쉽게 배울 수 있는 방법을 알려준다. 그 과정에서 수학이 진짜 탄생하게 된 이유나 알파고를 만들 수 있는 원리를 쉽게 전달하고 있다.
본 도서의 특징과 장점은 도서에 소개된 몇가지 문제를 풀어보면 금방 느낄 수 있다. 아래 보라색의 큰 정사각형은 분홍색 작은 정사각형 넓이의 몇배일까? 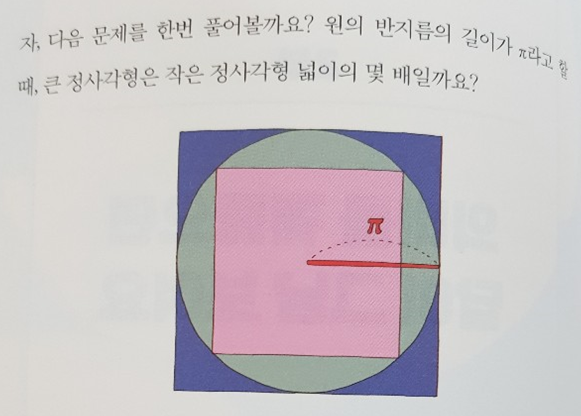
바로 답을 확인하지 말고 깊게 생각해 봤으면 좋겠다. 그리고 그동안 접근했던 방법이 아닌 프레임을 바꾸면 더 좋은 해결법을 찾을 수 있다는 것이 힌트라 할 수 있다.
해답은 다음과 같다. 불필요한 정보인 원을 없애버리고 2차원에 국한하지 말고 사각형을 돌려버린다면 직관적으로 작은 정사각형이 절반의 크기임을 알 수 있다. 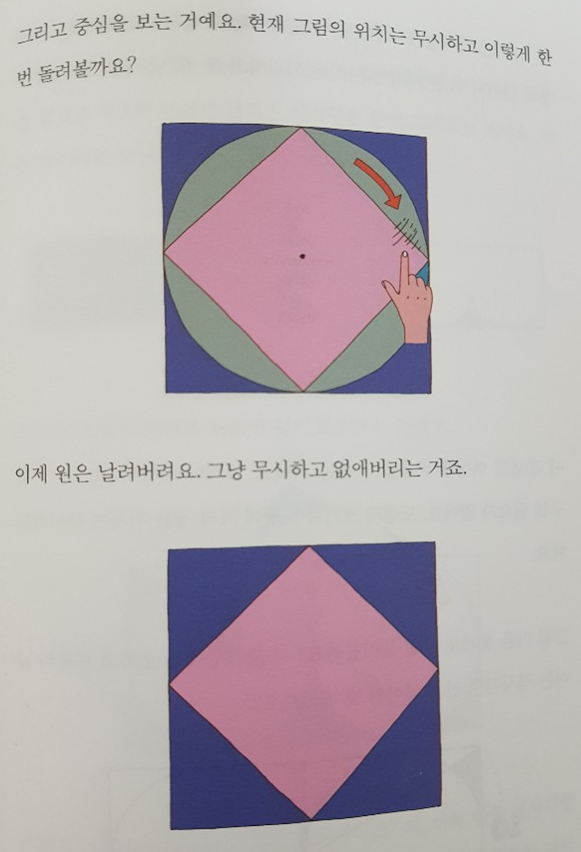
다른 문제를 더 살펴보자. 아래 그림의 숫자는 각 행이나 열의 숫자를 합한 값이다. 물음표의 값은 무엇일까? 참고로 이 문제는 프레임만 바꾸면 5초도 걸리지 않고 풀 수 있다. 
하지만 정규 교육과정을 거친 대부분의 사람은 연립방정식 위주의 방법으로 접근하게 될 것이다. 이 문제의 답은 너무 간단하여 본 리뷰에 소개하진 않겠다.
마지막으로 매우 간단해 보이지만 은근 쉽지 않은 덧셈 문제를 살펴보자. 
우리가 아는 상식으로는 제곱 연산자의 우선순위에 집착할 수 밖에 없다. 이를 기하학을 활용하여 직관적으로 접근하면 이런 멋진 답이 나온다. 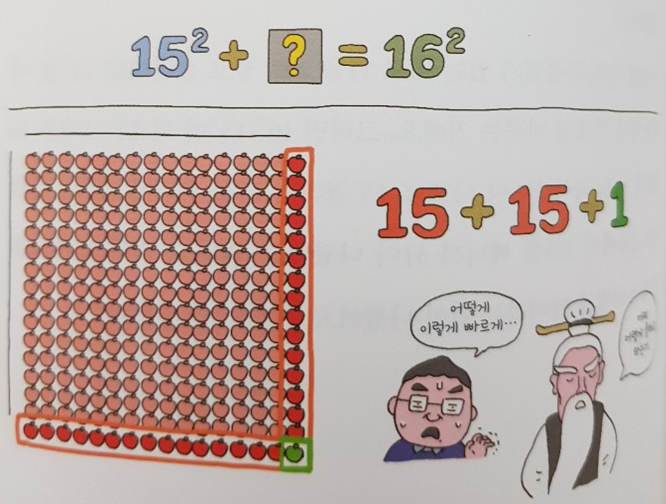
고작 세 문제를 설명했을 뿐이지만 이 책이 어떤 색을 띄는 수학 지침서인지 느낌이 와 닿을 것이라 생각한다. 직관과 프레임을 중시하는 접근법이 정말 마음에 들었다.
예를 들면 그 어렵다던 미분도 변화 유발자라는 개념을 통해 접근하는데 수학 교과서에서 느끼기 어려웠던 변화에 대한 개념을 생생히 느낄 수 있다. 미분을 배웠던 사람이라면 아래 그림 하나만으로 많은 것을 직관적으로 느낄 수 있을 것이다. 
수학에 이렇게 많은 논리와 매력이 숨어있는데 그저 계산만 할 줄 아는 수학이 어떤 의미가 있을까? 다행히도 이 책은 그런 수학에 담긴 진짜 의미를 쉽게 알 수 있도록 도와준다. 수학을 처음 접하는 아이들이나 학생들이 이 책으로 수학을 시작해야 하는 이유가 여기에 있다.
수학이 얼마나 재미있는지, 어떤 위력을 갖고 있는지, 진리에 다가가는 방법에는 무엇이 있는지, 지금까지 인류의 뛰어난 위인들은 이를 어떻게 접근하고 무에서 유를 창조했는지 알려주고 싶다면 적어도 우리나라에서는 깨봉 수학이 가장 빠른 지름길 인 것 같아 강력히 추천하고 싶다.
YES24 리뷰어클럽 서평단 자격으로 작성한 리뷰입니다.
