[리뷰] 그림으로 수학 잡는 깨봉수학교실 1
in Review on Review, Book, 수학, 기하학, 배수, 약수, 소수, 최소공배수, 최대공약수, Dna, 분수, 대소비교, 역수

동아시아 사이언스출판사의"그림으로 수학 잡는 깨봉수학교실 1(조봉한 저/신현호 편)"를 읽고 작성한 리뷰입니다.

이 책은 수학에 담겨진 진리를 깨우쳐 쉽게 익힐 수 있도록 도와주는 책이라 할 수 있다. 속도 위주에 계산 능력을 향상시키는데 주력을 두고 있는 초중고 정규 교과과정과는 사뭇 대조적이다.
책을 알게 된 계기는 이미 수학과 관련된 유명 유튜브 채널 깨봉수학을 접했기 때문이다. 말로 설명하는 것보다 링크를 클릭하여 아무 영상이나 시청해보면 그 의미를 알 수 있다. 어느 정도로 수학을 쉽게 가르쳐주는지, 더불어 그동안 우리가 수학에 몰랐던 원리가 얼마나 많이 담겨있는지 실감할 수 있다. 물론 관련 영상들은 책에 포함된 QR 코드를 통해서도 접할 수 있다.
최근 수학에 관심을 갖게 된 이유는 AI를 연구하기 시작하면서부터다. 기존 학교에서는 평가를 해야한다는 이유로 혹은 등수를 나눠야 한다는 이유로 우리에게 계산기가 되기를 강요했다. 때문에 정해진 시간에 빨리 풀 수 있어야 했고, 나아가 계산 기능을 향상 시키기 위해 그 속에 숨겨진 원리는 등한시하고 빠르게 공식을 외워야 하는 과제가 생겼다.
피타고라스 학파 이후로 수학이 지금까지 발전해 온 과정과 무에서 유를 창조하는 사고방식 그리고 엄밀한 증명속에 진리의 초석을 다지는 일이 수학의 진면목이라 할 수 있는데 그동안 공식외워서 문제 풀이 잘하는 계산기로 양성되어 왔으니 이로 인해 학생들의 불행은 물론 기초과학의 발전에도 악영향을 끼쳐온 셈이다.
AI에는 경사하강법이라는 개념이 나온다. 이미 다른 산업 분야에서 최적화라는 개념으로 활용되어 왔지만 그 근원이 어떻든 간에 인공지능을 학습시키는 핵심 개념이며 여기에 미분이 활용된다. 미분을 어떻게 활용하느냐에 따라 알파고와 같은 일류 바둑기사를 이길 수 있는 성능의 AI를 만들 수도 있는데 이런 세상을 바꾸는 원리를 찾아내는 능력이 우리에겐 부족하다. 그런 사고력이 부족하니 세상을 이끄는 창의성도 떨어진다.
이 책에 처음으로 등장하는 배수, 곱셈의 개념은 아래 그림처럼 사각형의 모양으로 등장한다. 사각형에는 가로, 세로 축이 존재하므로 이 두수를 곱한 것이 사각형의 면적이 되고 모양을 형성한다. 곱셈을 대수적으로 추상적으로 인지하는 것 보다 나이가 어릴수록 추상화 능력이 떨어질수록 이런 시각적 자료를 이용해 기하학적으로 접근하는 것이 유리하다. 지금 교육과정은 어떤지 모르겠는데 우리 세대들은 곱셈을 대수적으로만 접근했고 그 사소한 문제로 많은 친구들이 수학에 대한 흥미를 잃었다. 
저자는 우리 교육과정에 포함되지 않은 미국과 같은 기초학문이 튼튼한 나라의 원리 및 역사 그리고 본인 스스로 AI 전문가가 되기 까지 익혀온 인사이트를 접목하여 수학을 쉽게 배울 수 있는 방법을 알려준다. 그 과정에서 수학이 진짜 탄생하게 된 이유나 알파고를 만들 수 있는 원리를 쉽게 전달하고 있다.
이 책은 시리즈로 구성되며 그 중 첫번째 책이라 할 수 있다. 1권에 담긴 가장 중요한 개념은 수의 DNA라는 개념이다. 우리는 소수를 배울 때 그저 자기 자신과 1로만 나눌 수 있는 수라고 배웠다. 대체 소수를 왜 찾아야 하고 왜 중요하며 왜 배워야 하는지 그리고 배워서 어디에 쓸 수 있긴 한건지 이런 것들을 배우지 않고 그저 선택지에서 소수를 고를 수 있는 능력만 훈련받은 것이다.
비유하자면 아이들이 블록으로 장난감을 만들때 블록은 보통 세모, 네모, 동그라미, 별 모양 정도로 몇가지 유형이 정해져 있다. 이 중 세모를 여러번 쌓아 더 큰 세모도 만들 수 있지만 평행 사변형이나 마름모 모양을 만들 수 있다. 바로 그런 모양 자체를 즉 기초를 잘 알아두면 더 큰 확장과 새로운 세계를 창조해 낼 수 있다.
그리고 조금 더 나아가면 철학이나 컴퓨터에서 다루는 객체 개념도 익힐 수 있다. 예를 들면 세상에 사람은 존재하지 않는다. 다만 실체화된 영희, 철수가 존재한다. 이들을 사람이라 추상화하여 말한다. 사람은 나름의 특징이 숨어있지만 이 세상에 구체화 된 모습은 다양하다. 우리는 사람이 무엇인지 알지만 사람을 하나의 모습으로 그릴 수는 없다.
소수는 바로 그런 수이다. 아래 그림과 같이 백만은 DNA가 2와 5로만 구성되어 있다. 반면 15는 3과 5로 구성되어 있다. 수학의 세계에서 DNA는 소수이다. 이 간단한 사실 만으로도 DNA가 서로 달리 구성된 두 숫자간의 딱떨어지는 나눗셈은 불가하다는 것을 책에서는 알려준다. 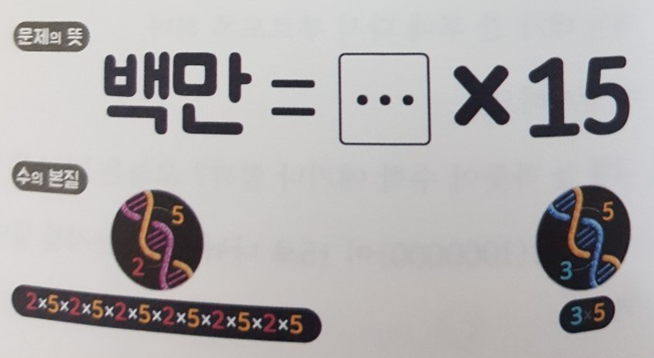
소수의 신비는 여기에서 그치지 않는다. 아래 그림을 보면 소수를 찾음으로 두 수의 공배수를 얼마나 쉽게 찾을 수 있는지 알 수 있다. 

최대 공약수, 최소 공배수 또한 마찬가지다. 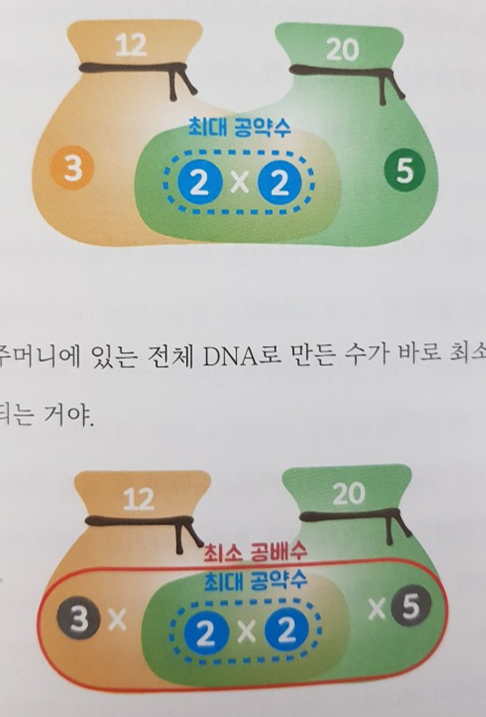
이렇게 1 ~ 100 사이에 숨은 모든 소수를 찾는 과정을 통해 배수와 약수의 원리도 알 수 있다. 
소수를 찾은 결과는 아래 그림과 같은데 이것이 밀레니엄 7대 난제 중 악명 높은 리만가설의 첫 출발지 “에라토스테네스의 체“이다. 
초등 수학이라고 우습게 볼 것이 아니다. 다 알고 있다고 자부하는 어른들도 이 책을 본다면 몰랐던 사실에 놀라게 될 것이다. AI와 같은 수학과 관련된 분야에 종사한다면 본인에게 직접적인 도움이 될 수 있음은 물론 그렇지 않은 사람일지라도 창의성, 논리력을 키우는 기회가 될 수 있으며 특히 자녀를 둔 아이에게는 수학의 묘미를 제대로 알려줄 수 있는 나침반이 될 수 있을 것이다.
수학에 이렇게 많은 논리와 매력이 숨어있는데 그저 계산만 할 줄 아는 수학이 어떤 의미가 있을까? 다행히도 이 책은 그런 수학에 담긴 진짜 의미를 쉽게 알 수 있도록 도와준다. 아이들이 이 책으로 수학을 접해야 하는 이유가 여기에 있다.
아이에게 수학이 얼마나 재미있는지, 어떤 위력을 갖고 있는지, 진리에 다가가는 방법에는 무엇이 있는지, 지금까지 인류의 뛰어난 위인들은 이를 어떻게 접근하고 무에서 유를 창조했는지 알려주고 싶다면 적어도 우리나라에서는 깨봉 수학이 가장 빠른 지름길 인 것 같아 강력히 추천하는 바이다.
YES24 리뷰어클럽 서평단 자격으로 작성한 리뷰입니다.
